Redakcja Bieganie.pl

Przedstawiamy obszerne fragmenty ciekawego artykułu, który ukazał się na łamach New Studies in Athletics (wydawnictwo IAAF) autorstwa czwórki japońskich naukowców. Dotyczy ona biomechanicznej analizy biegu na 10 tys m w Osace, a dokładnie trójki, która zajęła miejsca od 1 do 3: Bekele, Sihine, Mathathi. Często u nas na forum toczone są debaty o wadze techniki i efektywności biegu czy wykorzystania energii, może ten artykuł będzie zatem jakimś przyczynkiem do lepszego zrozumienia praw rządzących sposobem w jaki biegają najlepsi na świecie.
Artykuł napisali:
Prof. Yasushi Enomoto, profesor
nadzwyczajny Uniwersytetu w Kioto, członek Komitetu Naukowego Stowarzyszenia
Federacji Lekkoatletycznych w Japonii.
Mgr Hirosuke Kadano, absolwent
Wychowania Fizycznego i Sportu na Uniwersytecie Tsukuba w Japonii.
Mgr Yuta Suzuki, absolwent
Wychowania Fizycznego i Sportu na Uniwersytecie Tsukuba w Japonii.
Tetsu Chiba, nauczyciel szkolny w
Prefekturze Osaki.
Keiji Koyama, absolwent
Wychowania Fizycznego i Sportu na Uniwersytecie Juntendo, Chiba, Japonia.
Celem niniejszego badania było
zanalizowanie biomechanicznych właściwości ruchu najlepszych na świecie
biegaczy dystansowych – a konkretnie obserwacja 3 pierwszych zawodników finałów
na 10 000m w Mistrzostwach Świata w Lekkiej Atletyce w 2007 w Osace.
Metody
Aby dokonać analizy ruchu,
sfilmowano biegaczy na określonym odcinku bieżni w czasie finałowego biegu
na 10 000m w Mistrzostwach Świata w Lekkiej Atletyce w 2007. W tym celu
wykorzystano dwie kamery cyfrowe (60Hz) – jedną nagrywającą zawodników z
boku, drugą – z przodu. Inna kamera podążała za zawodnikami przez cały bieg –
nagranie z tej kamery wykorzystano do obliczenia międzyczasu na każde 100m.
Prędkość biegu oraz częstotliwość
kroku wyliczono z czasu na każde 100m oraz średniego czasu jednostkowego (dwa kroki) na każde 100m. Długość kroku
wyliczono poprzez podzielenie prędkości biegu przez częstotliwość kroku.
Ruch trzech prowadzących
zawodników zanalizowano na 5 etapach wyścigu: 600m (Etap 1), 3800m (Etap 2),
6200m (Etap 3), 8200m (Etap 4), i 9400m (Etap 5). Wykorzystano trójwymiarową
technikę analizy ruchu.
Po obliczeniu trójwymiarowych
współrzędnych oraz wyrównaniu współrzędnych za pomocą cyfrowego filtru
Butterworth’a, obliczono środek masy ciała, kąty, prędkości kątowe segmentów i
stawów kończyn dolnych oraz energię mechaniczną całego ciała. Wskaźnik
efektywności wykorzystania energii mechanicznej jeśli chodzi o prędkość biegu
obliczono poprzez podzielenie translacyjnej energii mechanicznej ciała przez
pracę mechaniczną w cyklu (Enomoto, 1997) obliczoną z sumy zmiany energii
każdego segmentu w każdym przedziale czasu (Metzler, 2002).
Wyniki i omówienie
Pierwsze miejsce w biegu zajął
Kenenisa Bekele (Etiopia), rekordzista świata w biegu na 10 000m. Drugie
miejsce – Sileshi Sihine (Etiopia), a trzecie – Martin Irungu Mathathi (Kenia).
Czas Bekele wszedł do 100 najlepszych czasów w historii (był to również
najlepszy jego wynik w sezonie) – pomimo wysokiej temperatury (30stopni
Celsjusza) i wysokiej wilgotności (65%) panującej w ten dzień w Osace.
| Miejsce | Zawodnik | Wzrost (cm) | Waga (kg) | Wynik w Osace | Życiówka |
| 1 | Bekele | 160 | 54 | 27:05.90 | 26:17.53 |
| 2 | Sihine | 171 | 55 | 27:09.03 | 26:39.69 |
| 3 | Mathati | 167 | 52 | 27:12.17 | 27:08.42 |
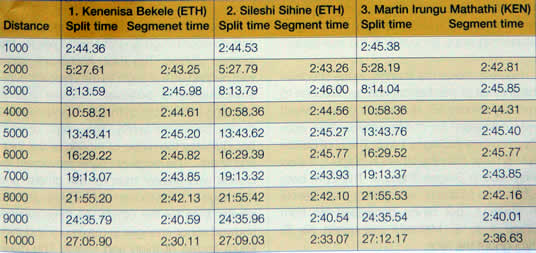
Poniższa Tabela przedstawia międzyczasy
oraz czasy odcinków na każde 1000m dla każdego z analizowanych zawodników. Na
pierwszych 9kilometrach, międzyczasy dla każdego z 3 lekkoatletów były prawie
takie same. Na 9km wszyscy trzej pojawili się razem. Oczywiście odnotowano
różnice w czasach na ostatnich 1000m, jednak były one stosunkowo małe. Prowadzący
nagle przyspieszyli na linii 8800m. Bekele biegł za Mathathi’m i Sihine’m,
jednak nagle dramatycznie przyspieszył na ostatnim okrążeniu i pozostawił
przeciwników w tyle. Czasy ostatniego okrążenia wyglądały następująco: 55.51 –
Bekele, 58.66 – Sihine, i 62.16 – Mathathi.
Poniższe wykresy przedstawiają średnią
prędkość biegu, częstotliwość kroku oraz długość kroku na każde 400m dla
każdego z trzech omawianych zawodników. Do 9km różnica w częstotliwości kroku
czy długości kroku była niewielka. Elliot i Ackland (1981) udowodnili, że spadek
prędkości biegu jest spowodowany spadkiem częstotliwości kroku. Z kolei,
Williams (1991) wykazał, że pod wpływem zmęczenia, biegacze zmniejszają długość
kroku biegnąc z tą samą prędkością. Dane z omawianego biegu nie wykazały
żadnych istotnych zmian w czasach – trzej czołowi zawodnicy biegli tak jakby
nie odczuwali zmęczenia w czasie biegu mimo wysokiej temperatury i parnych
warunków pogodowych.
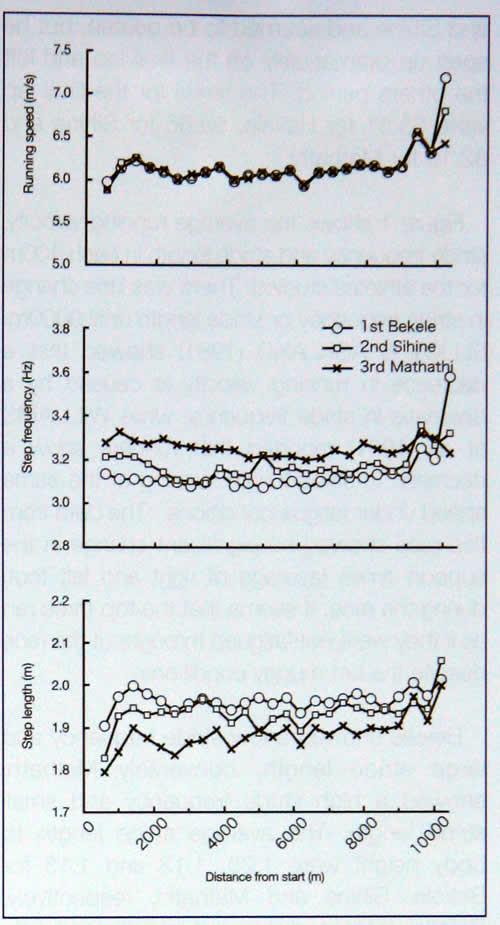
Bekele wykazywał niską
częstotliwość kroku i dużą długość kroku. Methathi przeciwnie – wysoką
częstotliwość kroku i małą długość kroku. Średni stosunek długości kroku do
wysokości ciała dla trzech omawianych zawodników wyglądał następująco: 1.23 –
Bekele, 1.13 – Sihine, oraz 1.13 – Mathathi. Bekele zwiększył swoją prędkość
poprzez znaczne zwiększenie częstotliwości kroku na ostatnim okrążeniu.
Współczynniki korelacji prędkości biegu do częstotliwości i długości kroku
przedstawiały się następująco: 0.904 oraz 0.662 – Bekele, 0.753 i 0.492 –
Sihine, oraz 0.377 i 0.717 – Mathathi. Te wyniki dowodzą, że Bekele mógł
utrzymać dużą długość kroku i zmienić prędkość biegu poprzez zmianę
częstotliwości kroku, szczególnie na ostatnim okrążeniu.
Poniższy wykres przedstawia zmiany
wskaźnika efektywności wykorzystania energii mechanicznej w stosunku do
prędkości biegu (EI) oraz średniej mocy obliczonej poprzez podzielenie pracy
mechanicznej przez czas jednostkowy w etapach 1 i 5. Prędkość biegu Bekele w
pierwszym etapie była mniejsza niż pozostałych zawodników, później wzrosła w
etapie trzecim i piątym. Prędkość biegu zarówno Sihine’go jak i Mathathi’ego w
pierwszym etapie była większa niż Bekele’go. U Sihine prędkość biegu spadła w
etapie czwartym i piątym. Natomiast Mathathi utrzymywał prędkość w czasie
biegu.
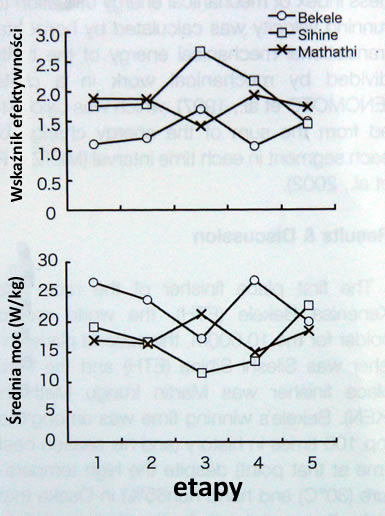
Średnia moc w czasie biegu nie
była stała. Średnia moc Bekele’go w etapie 1 i 2 była większa niż u dwóch
pozostałych zawodników. Te wyniki dowodzą, że ruch Bekele’go wymagał więcej
energii, jednak Bekele zwiększył swoją efektywność aby utrzymać prędkość biegu,
a następnie przyspieszył na końcowym okrążeniu. Mathathi być może miał dobrą
technikę biegu wykorzystującą skutecznie energię mechaniczną, jednak pod koniec
biegu nie był w stanie wydobyć z siebie większej energii na przyspieszenie.
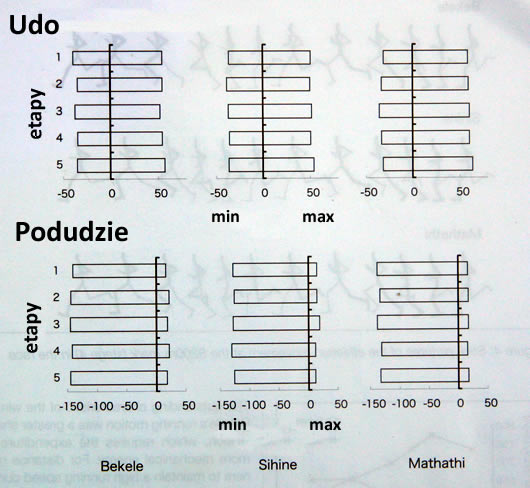
Poniższy wykres przedstawia zmiany
maksymalnych i minimalnych kątów odchylenia uda i podudzia. Kąt odchylenia uda i podudzia został określony
jako kąt odchylenia od pionu (zgodnie z ruchem wskazówek zegara – kąt dodatni).
Dodatni kąt odchylenia oznacza wymach w przód, ujemny – oznacza wymach w tył.
Długość każdej kreski wskazuje zakres ruchu podudzia i uda. Zakres ruchu
podudzia u Bekele’go był większy niż u pozostałych dwóch biegaczy. Z kolei,
zakres ruchu uda u Mathahi’ego był większy niż u pozostałych dwóch zawodników.
Wszyscy trzej lekkoatleci wykazali niewielkie zmiany maksymalnych i minimalnych
kątów uda i podudzia. Maksymalny kąt uda i zakres ruchu uda u Mathatthi’ego
stopniowo wzrastał, natomiast u pozostałych dwóch sportowców – nie ulegał
zmianie. Maksymalne i minimalne kąty podudzia u Bekele’go utrzymywały się na
stałym poziomie, natomiast u dwóch pozostałych biegaczy – malały.
Kolejny rysunek to obrazki
przedstawiające ruch trzech zawodników na linii 8200m (Etap 4). Cienkie linie
obrazują lewą stronę ciała. Obrazek Bekele’go pokazuje, w początkowej fazie
biegu jego podudzie sięgało uda, czego konsekwencją było zmniejszenie
minimalnego kąta kolana. Później, przed uderzeniem stopą o ziemię podudzie
wędrowało coraz bardziej w przód.

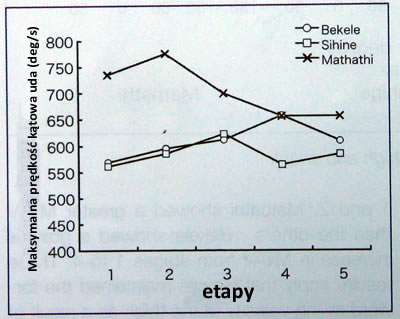
Ostatni wykres pokazuje zmiany w
maksymalnej prędkości kątowej uda (MTAV). Na etapie 1 i 2, Mathathi wykazywał
większą maksymalną prędkość kątową uda w porównaniu z pozostałymi dwoma
biegaczami. U Bekele, na etapach od 1 do 4,
maksymalna prędkość kątowa uda stopniowo wzrastała. Te wyniki dowodzą,
że Bekele dzięki kontroli ruchu podudzia utrzymywał prędkość wymachu uda w przód,
co może być cechą charakterystyczną tego zawodnika. Enomoto i Ae (2005)
twierdzą, że kenijscy biegacze szybciej wymachują udem w przód dzięki dużemu
zakresowi zgięciu kolana. Twierdzą także, że wymach uda w przód to jeden z
kluczowych ruchów u biegaczy dystansowych.
Podsumowując, u trzech
najlepszych zawodników finałów na 10 000m w czasie Mistrzostw Świata w
Lekkiej Atletyce w 2007 w Osace zaobserwowano tylko niewielkie zmiany w ruchu w
czasie biegu oraz znikome objawy zmęczenia mimo ciężkich warunków pogodowych.
Niezwykłą cechą zwycięzcy, Bekele, był ruch w czasie biegu, a dokładnie,
intensywniejszy ruch podudziem, który wymaga większych wydatków energii
mechanicznej. W przypadku biegaczy dystansowych, utrzymywanie wysokiej
prędkości biegu oraz wykorzystanie sprintu w końcowym etapie wymaga nie tylko
efektywnego wykorzystania energii mechanicznej, ale także umiejętności
wygenerowania w odpowiednim momencie większej energii mechanicznej – podobnie
jak u sprinterów.
REFERENCJE
Elliot B, Ackland T.
Biomechanical effects of fatigue on 10,000 meter running technique.
Res Q Exerc Sport. 1981 May;52(2):160-6
ENOMOTO YASUSHI, AE MICHIYOSHI, OKADA HIDETAKA, FUJII NORIHISA.
Running technique in long distance running and the effectiveness of mechanical energy utilization.
Japanese Journal of Biomechanics in Sports & Exercise
VOL.3;NO.1;PAGE.12-19(1999)
Yasushi Enomoto, Michiyoshi Ae
A BIOMECHANICAL COMPARISON OF KENYAN AND JAPANESE
ELITE LONG DISTANCE RUNNER’S TECHNIQUES
K.R. Williams, R. Snow, C. Agruss
Changes in Distance Running Kinematics with Fatigue
International Journal of Sport Biomechanics 1991:7 p138-162
V Metzler, A Arampatzis, G-P Bruggemann
Influence of 2D and 3D body segment models on energy calculations during kinematic analysis of running
European Journal of Applied Physiology (2002), 86; 337-341